Welcome back to Back To Basics, our journey to master electronics one little bit at a time.
So far, we have covered the essentials: safety, basic tools of the trade, and the important Ohm’s law, the foundational relationship between voltage, current, and resistance.
But what happens when circuits get more complex than a single resistor? What about parallel branches, multiple power sources, or a complex resistive network? We need a bigger, better set of rules. Today, we’re introducing the two most powerful, indispensable rules in circuit analysis: Kirchhoff’s Laws.
Named after physicist Gustav Kirchhoff, these laws are the foundation for everything we do next. By the end of this video, you’ll be able to analyze any basic series or parallel circuit and understand how energy and charge are conserved inside the wires.
KCL
Let’s start with the simplest concept, the one you can’t argue with: Kirchhoff’s Current Law, or KCL. KCL is all about the conservation of electric charge. It states that: The algebraic sum of currents entering a node (or junction) must be equal to the algebraic sum of currents leaving that node.

Think of it as a plumbing pipe junction, or a traffic merge lane. If you have 5 Amperes of current flowing into the junction, you must have 5 Amperes flowing out across all the outgoing paths. Charge can’t just pile up or disappear in a wire—it must be conserved. Simply put: What comes in must come out!

We call the meeting point of three or more wires a node. Mathematically, we express this as: The sum of currents entering the node equals the sum of currents leaving the node.

Let’s look at this simple parallel circuit.

We have a total current It leaving the battery. When it hits the first parallel junction (the node), it splits into two branch currents, I1 and I2. KCL immediately tells us that the total current is the sum of the branch currents.
So, It = I1 + I2. And here is the clever part: at the next node, I1 and I2 meet up again to form the original total current It, as it returns to the battery. KCL is your sanity check for all parallel circuits.
KVL
Let’s now talk about the other law, which is about the principle of energy conservation in a circuit: Kirchhoff’s Voltage Law, or KVL.
KVL governs the voltages around a closed loop—any path that starts and ends at the same point.

KVL states that: The algebraic sum of all the voltages around any closed loop in a circuit is equal to zero.
To understand the meaning of this statement, let’s use another analogy. Imagine a roller coaster, which works based on the physics concept of potential energy. The battery (the voltage source) is the lift hill that gives the car potential energy—a voltage rise. The resistors are the dips, loops, and brakes that use up or drop that energy—the voltage drops. When the car returns to the loading platform, its net change in height—its net potential energy—is zero.

In a circuit loop, the energy supplied by the source must be completely dropped across the components. If we trace the entire loop, the sum of voltage rises and drops must be zero.
In this simple series circuit, we have a source voltage (VS) and three resistors with voltage drops V1, V2, and V3 across them. If we trace the loop, always in the same circular direction representing the flow of the current, going from the negative to positive terminal of the battery is a rise, and going across each resistor in the direction of current flow is a drop.
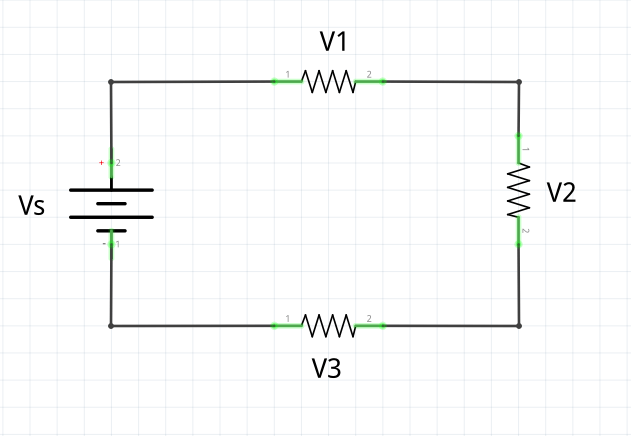
KVL says:
Vs -V1 – V2 – V3 = 0
Rearranging this equation shows us that the source voltage is exactly equal to the sum of the voltage drops:
Vs = V1 + V2 + V3
KVL is the reason why the voltage splits up in a series circuit. The total energy has to be accounted for, and it must balance out to zero when you return to the start. If your KVL equation doesn’t equal zero, you’ve made a mistake!
Circuit Analysis Application
Now for the fun part: let’s put KVL, KCL, and our trusty Ohm’s Law together. This is where you unlock your circuit analysis superpower.
Here is a classic intermediate circuit: a series resistor, followed by two parallel resistors, all connected to a battery. We cannot simplify this down to a single equivalent resistance as easily. So… what do we do?
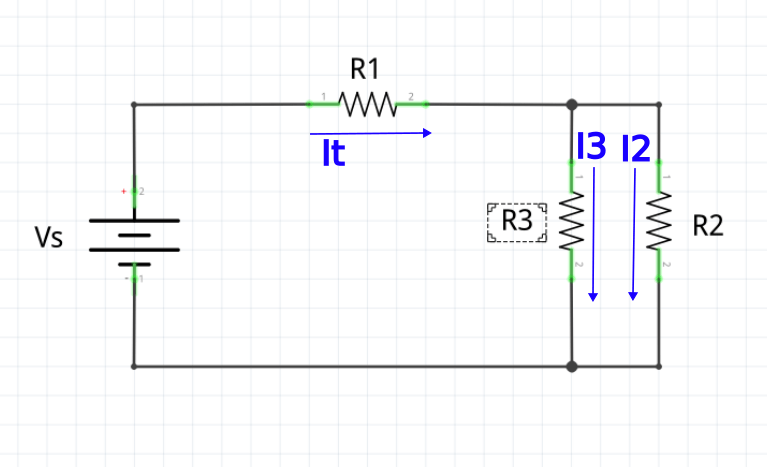
First, we look at the main node where the total current (IT) splits. KCL immediately gives us our first equation:
It = I2 + I3
Next, we apply KVL to the main loop. We have one voltage rise (Vs) and three drops: across R1, R2, and R3. Wait, we only need to account for the components in the loop.
Let’s apply KVL to the outer path: The source voltage minus the drop across R1 minus the drop across R2 must equal zero.
Vs – VR1 – VR2 = 0
And here’s the trick. We use Ohm’s law, V = IR, to replace the voltage drops with their corresponding currents and resistances.
Since It flows through R1 and I2 flows though R2, our final KVL equation becomes:
Vs – (It * R1) – (I2 * R2) = 0
Now we have two equations,
It = I2 + I3 and
Vs – (It * R1) – (I2 * R2) = 0
and we can create a third for the second inner loop:
Vs – (It * R1) – (I3 * R3) = 0
By substituting and solving this system of linear equations, we can find any unknown current or voltage in the circuit! This is the power of Kirchhoff’s Laws.
Conclusion
Today, we have learned that all complex circuits follow two simple, unbreakable rules: Charge is conserved (KCL), and energy is conserved (KVL). These are the cornerstone principles that every electrical engineer and technician uses daily.
In the next episode of Back To Back, we are going to examine a new component that can be used in electronic circuits: the capacitor. From there, a whole new world will open to us, filled with voltages and currents that change over time and can be used for many, many applications.
Happy experiments!!!
Companion Video: