Author: eleneasy.com

I am an old school electronics engineer, but I worked almost forever doing software development for the big telecommunication companies suppliers. I have recently decided that it was time to start digging into my old knowledge and make a hobby out of it. I have several subjects in mind that I would like to explore: robotics, electronic musical instruments, home automation, and so forth. Let’s make this journey together! We can surely learn a lot of new things from each other. Drop me a comment! I look forward to hear your thoughts!

Back To Basics Episode 7: Everything You Need To Know About Inductors


In the last episode, we talked about the capacitor—the component that stores energy in an electric field and hates it when voltage changes. Today, we meet its magnetic twin.


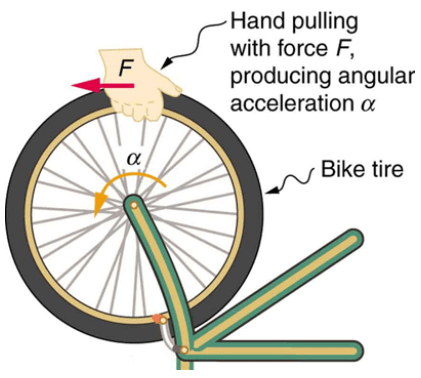
If I try to spin a wheel instantly, I cannot do it. Since the wheel has a mass, it has inertia and so it resists being moved. However, once it is finally spinning, if I try to stop it suddenly…. again, it fights me and prevents me from doing it.


In the world of electronics, we have a component that does exactly the same thing, but with the current. Like the capacitor tries to keep a constant voltage at its leads, the inductor tries to keep constant the current that flows through it with the help of a magnetic field.


It is the most stubborn component in a circuit. It is basically the mass of a circuit. If current is not moving through the wire, it doesn’t want it to start. If current is already moving through the wire, it doesn’t want it to change, or even stop.


Today, we are going to look at the physics of the inductors, why they can be dangerous, and how they are used in real world applications.


Anatomy of an inductor


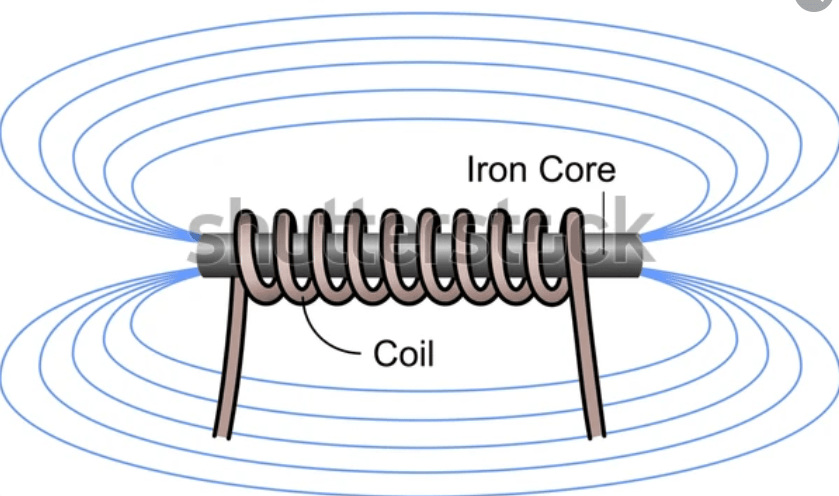
Physically, an inductor is the simplest component you’ll ever see. It is usually just a coil of wire. But don’t let the simplicity fool you.


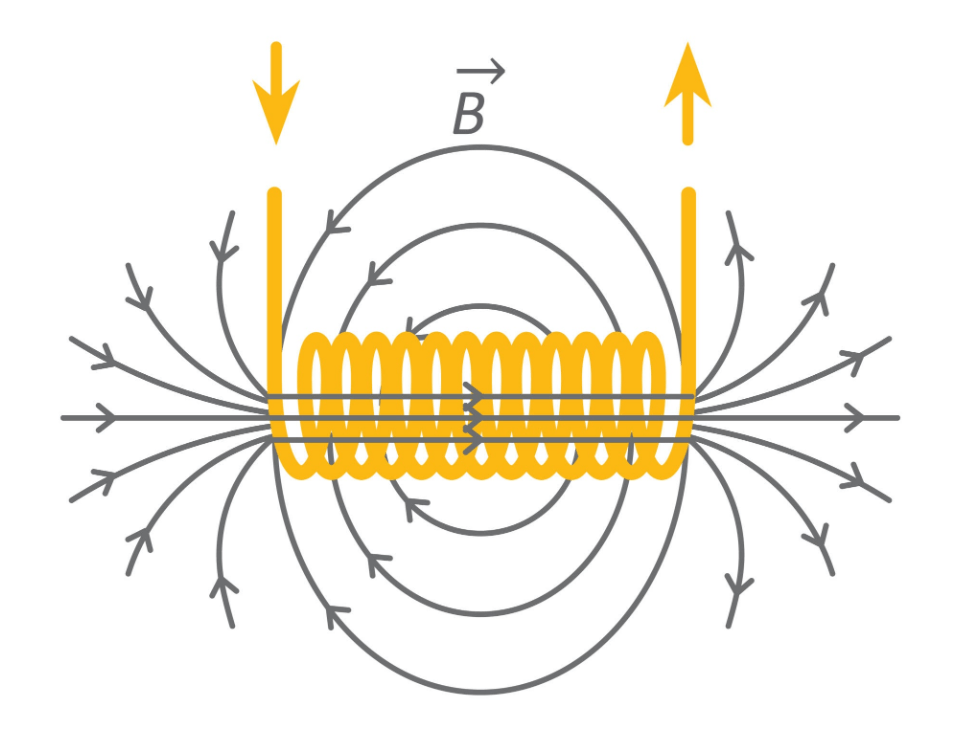
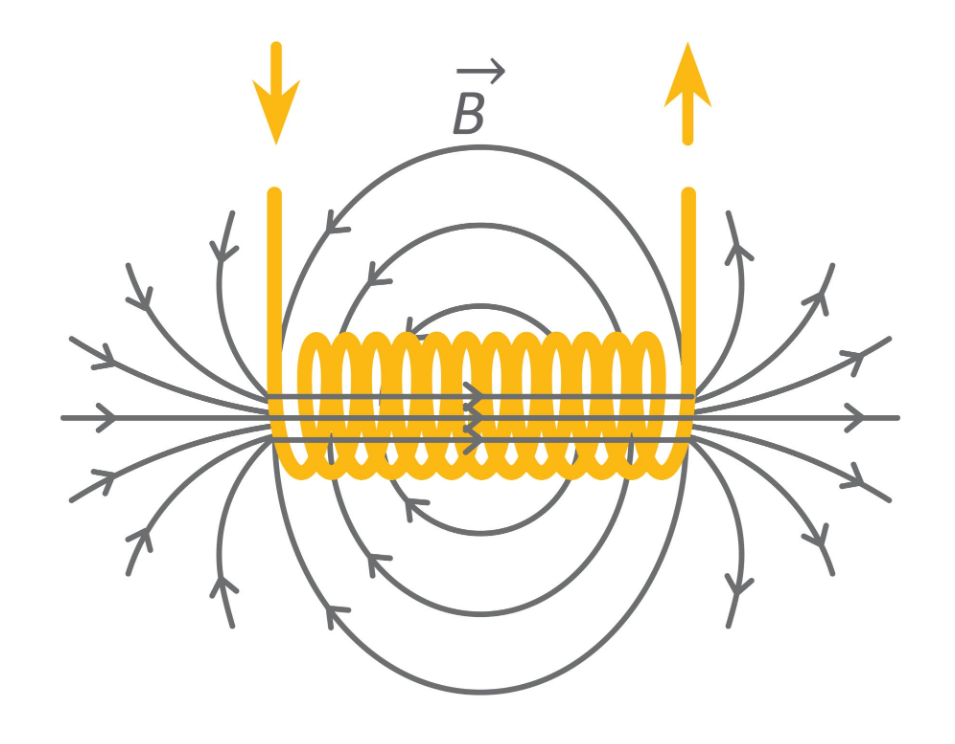
When current flows through a straight wire, it creates a small magnetic field around it. But when we wind that wire into a coil, a shape that we call solenoid, those individual fields stack up and reinforce each other.


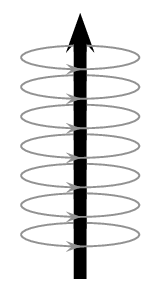
This creates a concentrated magnetic field through the center of the coil. And this is where the energy lives. While capacitors store energy in an electric field between plates, inductors store it in a magnetic field within the coil.
Additionally, what’s inside the coil matters just as much as the wire itself. We call the inside of the coil “core”.

If the core is made out of air, the strength of the field is low, and such inductors are normally used for high frequency circuits.


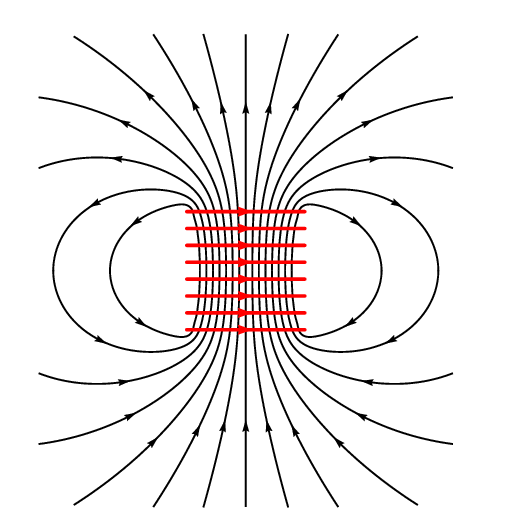
If the core is made of iron or similar ferromagnetic material, it will channel the magnetic flux and will intensify it, making the inductor capable of storing a much greater amount of energy.


If the core is made of ferrite, which is a ceramic like material containing usually silicon and iron, then the inductor acquires a much faster capability of switching from on to off and viceversa without the energy loss that we would get with solid iron.


The ability of the coil to store energy in a magnetic field is called inductance, and it is measured in Henry, named after Joseph Henry, who discovered this property around the same time as Michael Faraday. The measure Henry is indicated with the capitol letter H.


How the inductor works


So, why the inductor resists to current changes? It comes down to a fundamental rule of physics called Lenz’s law.


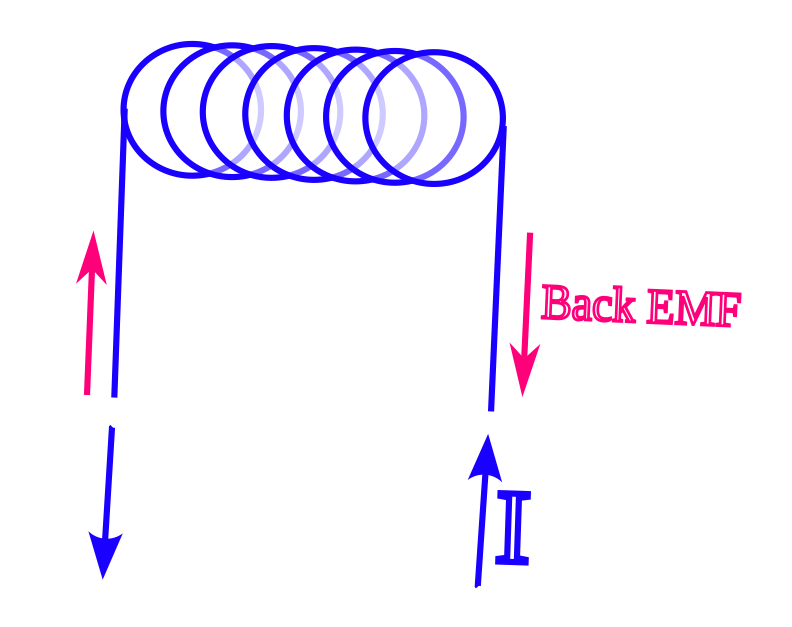
When we try to increase the current through an inductor, the magnetic field has to expand. But the expansion actually pushes back against the incoming current. We call this Back EMF, or Back Electromotive force. It’s basically like trying to push a heavy car: it takes a lot of effort just to get it rolling.


Let’s look at the math, but don’t let that scare you. It is just a way to describe the stubbornness of the inductor.

The voltage V across an inductor is defined by

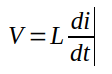
where L is the inductance and di/dt is simply the speed at which the current is changing.
Here is the magic: when we try to push current through, the magnetic field expands. According to Lenz’s law nature hates a change in magnetic flux. And so, the expanding field creates its own internal voltage, the back emf, that pushes back against the battery. It is literally an internal “ghost battery” fighting the actual battery.


Inductor behavior in DC vs. AC


Now, because inductors react to change, they behave totally differently depending on the type of electricity we feed them.


In a DC circuit, when we first flip the switch, the inductor fights the current. It acts like a wall, an open circuit. But, once the current is flowing steadily, the inductor gives up, it becomes just a regular piece of wire.


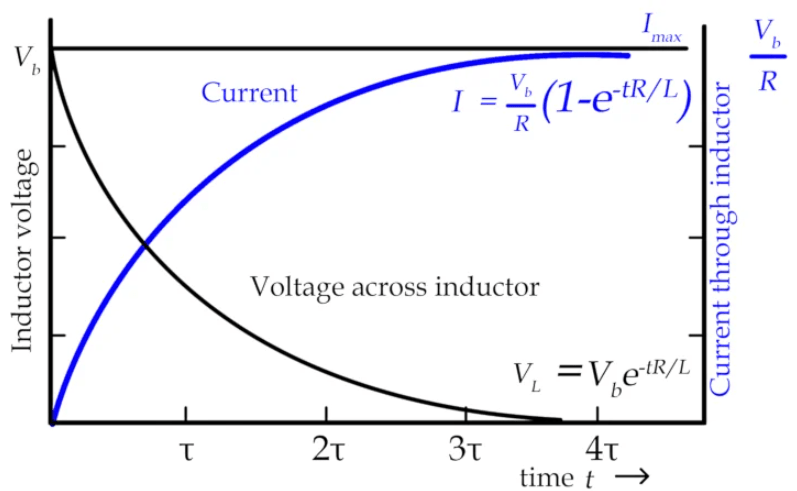
In an AC circuit, the current constantly changes direction. This means that the inductor is constantly fighting. We call this “fighting” Inductive Reactance. The higher the frequency of the AC, the harder the inductor fights it.


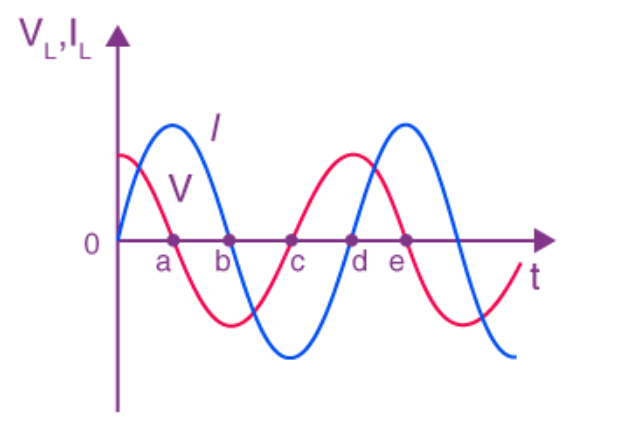
This makes them perfect for filtering out high frequency noise. They let the slow, steady power through, but block the high frequency noise. This is why you see those lumps on the laptop charging cables. They are actually inductors blocking the high frequency interference.


Real world applications

So, where do we actually use these things? Here are a few examples.


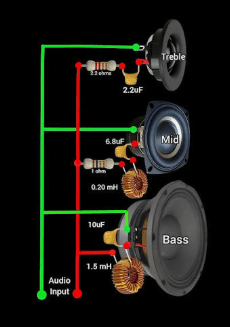
Filters: in the audio speakers inductors are used in crossovers to block high frequency sounds from reaching the woofer, ensuring it emits only those deep, clean, bass notes.


Chokes: used in power supplies to smooth out ripples in the current.


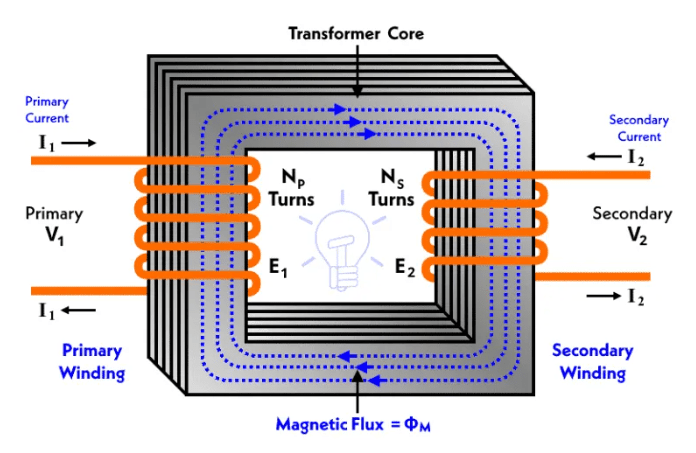
Transformers: if we put two inductors next to each other, the magnetic field of one can induce an EMF in the other. And that’s how they step power up or down for the electric distribution grid.


Buck converters: they are made with small transformers working at high frequencies.


Electromagnets: simple coils, usually winded around a ferromagnetic core, that becomes real strong magnets when we make a current flow through their wires. They are used all over the places. And they are especially common inside electric motors, like the ones that power many kitchen appliances.


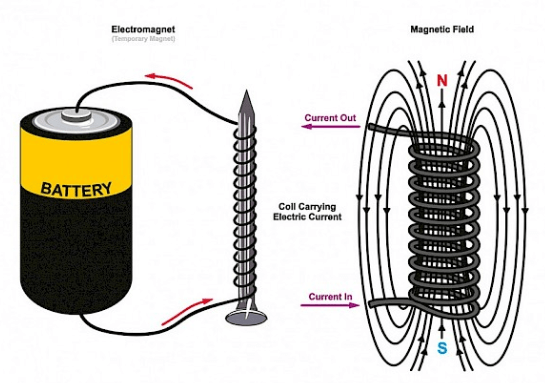
Sensors: have you ever seen those loop of wires buried under the asphalt at traffic lights? Those are inductors. When a car sits over them, it changes the inductance, telling the traffic lights circuitry that a car is there waiting for its turn to pass.


The inductive kickback


A word of warning now. Because an inductor wants to keep a constant amount of current, it can be dangerous at times.


If you have current flowing through a coil and you suddenly pull the plug, the magnetic field inside the coil collapses. But the energy in that magnetic field needs to go somewhere. What happens is that the inductor will convert that energy in a voltage spike with the polarity oriented in such a way that it will try to keep the current flow without a change.


Have you ever seen a spark when you suddenly disconnect a wire from a circuit where current was flowing through it? That spark is caused by this inductive kickback produced by the inductance in the circuit. When you open the circuit, the inductor will generate a voltage high enough to make the current go through the air around the disconnected wires, thus the spark.


In electronic circuits, the inductive kickback may damage the semiconductors in the circuit. In such a case, we use a diode, in parallel with the inductor, oriented in such a way that it will behave like a short circuit toward the back EMF of the kickback, and it will behave like an open circuit during normal operations.

Here is an example: a transistor controlling the coil of a relay. The diode in parallel to the coil will short the kickback which, otherwise, would destroy the transistor.

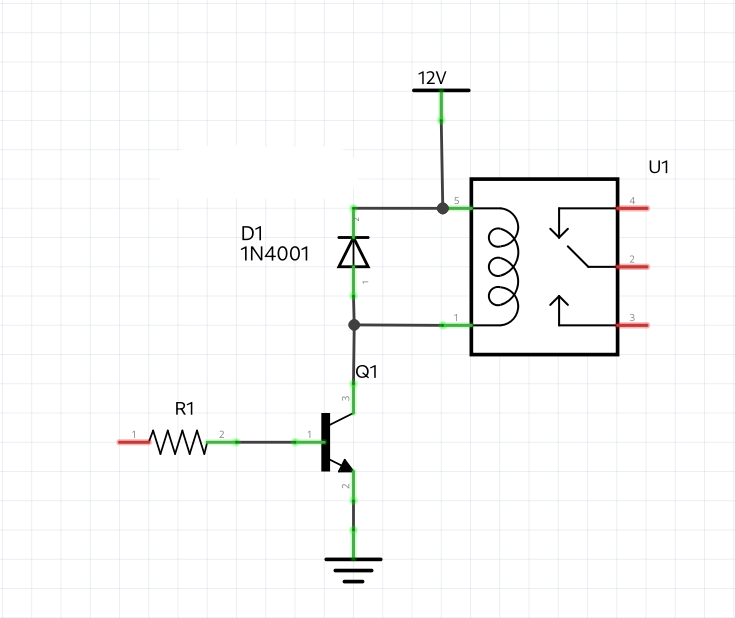
A diode connected like that is called flyback diode, because it will make the kickback fly away.


Inductor identification


Now that we know how inductors work, we need to know how to identify them on a circuit board. Unfortunately, this is trickier than it sounds, because inductors are masters of disguise.


Let’s start with the physical shape, and there are several of them.


The first kind of shape is the axial inductor: these look exactly like resistors. They are small, usually green of cyan, and have color bands.

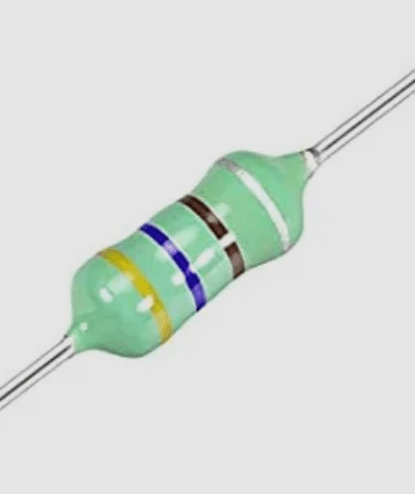
A pro-tip for you. If the body looks like a sea-foam green, then it is most always an inductor. If it is tan or blue, it is likely a resistor.


The second inductor shape is the drum or radial inductor. These look like little black mushrooms or weights. You’ll see the copper wire wrapped around a ferrite core, often covered in clear or black shrink wrap.


The next shape is the toroid. These are like small donuts. They look like a ring wrapped with wire. In this category we find usually high performance inductors used in power supplies.


Last category I would like to talk about is the one of the SMD inductors. On modern boards, these look like tiny gray or black ceramic rectangles. Unlike resistors, they are usually taller, since they need space for winding the coil.


Now, how do we figure out their inductance value? Well, just like resistors, inductors use a code system. Their base unit for these codes is almost always the microhenry.

Let’s start with the color code, used for axial inductors. It’s the same colors used for resistors: black for 0, brown for 1, red for 2, and so forth.

Inductors can have 3, 4, or 5 bands, like resistors, and they are read exactly the same way as the resistors.


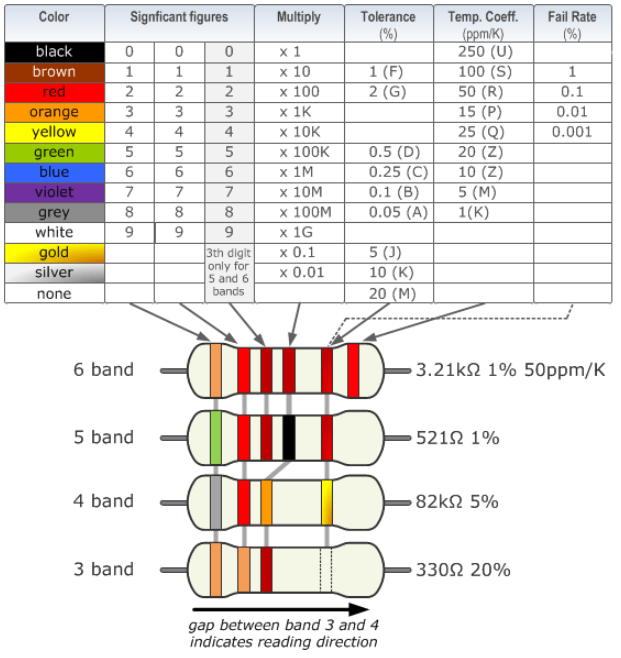
For example, the axial inductor from above has yellow, blue, black, and silver, which means 46 microhenry, and a tolerance of 10%.

Let’s now talk about the numerical code, present on the SMD and drum inductors. You might see a 3 digit number, like in the above drum indicor which shows on its case 101. The first two digits are the value, the third is the number of zeros after the first two digits.

This means that 101 translates to 10 + one zero, which means 100 microhenry.


Like with resistors and capacitors, if in doubt, don’t guess, measure the value. The problem is that multimeters usually do not have a mean to measure inductors. You can still test the resistance which, for good inductors, should be almost zero, since it is just a coil of wire.
If you want to really measure the value, you’ll have to acquire an instrument called LCR meter, which is a high specialized instrument that take only measurements of inductors, the letter L, capacitors, the letter C, and resistors, the letter R.


The essential starter kit


Now, if you want to start using inductors in your experiments, you don’t need to buy every inductor on the market. Inductors are expensive and bulky compared to resistors, so you want to be strategic. Here is my “starter kit” recommendation for any hobbyist lab.


Begin with a must-have assortment. Don’t start buying individual values. Go to Amazon or eBay and look for an Axial Inductor Assortment Kit.

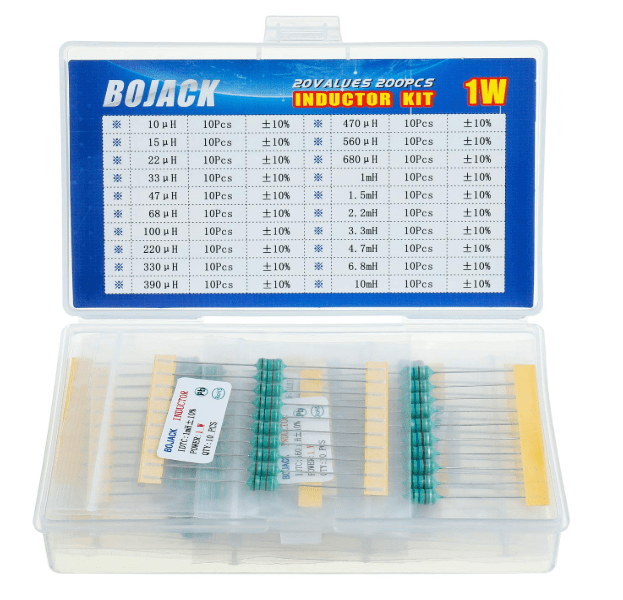
You’ll get usually 200 or 300 pieces in a small plastic box, with a bunch of different values.

They look like resistors, and fit perfectly into breadboards. The values usually range from 1 micro henry to 10 milli henry, and this covers about 90% of basic hobbyist filtering needs.


If you plan on building your own power regulators or buck converters, you will need toroidal inductors. Go with values like 10uH, 47uH, and 100uH to start with. Look for high current ratings, at least 2 or 3 amps. Power inductors are rated by how much heat they can handle before start having problems.


For noise management, you may also want to acquire a few ferrite bids. There aren’t technically coils, but they are essential. They are basically small cylinders of ferromagnetic material. You slide them over wires to choke out high frequency interference. If your project has a buzzing sound in the speakers or a flickering screen, a ferrite bead is often the cure.


Finally, if you are serious about inductors, a standard multimeter won’t cut it. Most cheap multimeters can’t measure inductance.
In such case, I recommend to pick up a cheap TC-1 Multi function tester, which you can find for about $20, and you can just plug an unknown inductor in, and it will tell you the value and the internal resistance instantly.


Better yet, buy a LCR meter, which will allow you to make precise inductance measurements, as well as capacitances and resistances. Some devices can even provide you with a full model for the component you are testing, giving you both its resistance, the series inductance, and the parallel capacitance, which is useful should you decide to work with high frequencies.


Conclusion

To summarize what we said so far:

inductors are everywhere. They are in your phone’s wireless charger, the crossover in your high end speakers, the massive transformers on your street corner, and so forth.

  • They store energy in a magnetic field.
  • They resist changes in current.
  • They are the high frequency blockers of the electronics world.

In our future videos of this series, we are going to continue our journey in the world of electronics, showing new types of components, and how to use them, as well as moving the first steps in designing you own circuits.
If you find this deep dive helpful, like it and subscribe.

I’ll see you in the next episode and, in the mean time…

Happy experiments!

Companion YouTube video:

Back To Basics Episode 6: The Absolute Beginners Guide To Capacitors


Welcome back to Back To Basics, our journey to master electronics one little bit at a time.


Think of your favorite gadget. Your phone, your laptop, even your car. Now, imagine if they just… stopped working. Not because the battery died, but because they couldn’t handle the noise of their own electricity.


Most people know about batteries but, today, we are talking about the unsung hero of the circuit board: the capacitor. It’s the component that can dump its entire energy load in a millisecond, smooth out a jagged power supply, and even keep your clock running when you pull the plug.


Today, in back to basics, we dive into the world of electrostatic storage. Let’s find out how these little cans and disks actually work.

What Is A Capacitor


Basically, a capacitor is a passive component that stores energy in an electric field. Unlike a battery, which uses a slow chemical reaction, a capacitor is all about speed.


To visualize this, imagine a plumbing system. If a battery is a huge water reservoir, a capacitor is a small pressure tank. It can’t supply water for hours, but if the main pump flickers for a second, the pressure tank kicks in instantly to keep the flow steady. It’s the ultimate shock absorber for electricity.


It is made of three main parts: two conductive plates, and an insulator in between, called a dielectric. When we apply voltage, positive charges pile up on one plate, and negative charges pile up on the other. The charges would like to reach each other, but the dielectric stops them. That tension is actually stored energy inside the capacitor in the form of an electric field generated by those charges.


We measure the ability to store charge in Farads. But, because a single Farad is actually a huge amount of energy, we most often use a small fraction of it: the millifarad, the microfarad, the nanofarad, and the picofarad.

Top Three Applications

Why do we actually use capacitors?

There are three big roles for them:

  • filtering and smoothing, where they turn bumpy DC voltages into a smooth and steady line.
  • energy storage, where they can provide a quick burst, for example for a camera flash or a subwoofer’s bass hit
  • signal coupling, where they allow AC signals, like music, to pass through a circuit, while blocking unwanted DC offset.


Now, not all capacitors are built the same. Here are three types that you’ll see the most often.


Ceramic capacitors: small, cheap, and non polarized, which means you can plug them either way. They look like little lentils and are perfect to deal with high speed filtering.


Electrolytic capacitors: these look like miniaturized soda cans. They hold a lot of energy but they are polarized, meaning they have a positive and a negative side. Hook them up backward, and things will get really messy. They are perfect for low speed filtering, for example in DC power supplies.


Film capacitors: Usually rectangular and green or red. These are very stable and great for audio circuits or high voltage power.

And, just to give you the full picture, here is a table I made where all the type of capacitors are listed.

In here, note that NP0 capacitors are a special kind of ceramic capacitors. Polystyrene and polypropylene are the typical dielectrics of film capacitors. Tantalum capacitors are a type of electrolytic capacitors, where the positive plate uses tantalum metal, and the dielectric is made oxidizing one side of the tantalum plate. As the other kind of electrolytic capacitors, these are also polarized.

Identify The Codes

OK, let’s say now we got a bunch of capacitors, all there sitting on the workbench. But how do we know which one is which? Unlike resistors, which use color bands, capacitors use numbers and letters printed on their body. The big problem is, different types of capacitors don’t speak the same language. And… yes, sometimes even same type capacitors don’t.

Let me tell you the most common ways to interpret the information on the capacitors cases.

And let’s start with electrolytic capacitors. They are the most straightforward, because they are physically larger, and the manufacturers have enough room to print the actual values directly on the side.

The capacitance is a number followed by the Greek letter mu and a capitol F, which stand for microfarads. For example, this one says 100uF. No math required.

Follows the maximum voltage rating, in this case 50V. Remember that you have to always use the capacitor at a voltage smaller than the rated voltage, or you’ll damage the capacitor.

Last, we have the polarity, this big stripe with the minus sign. That stripe indicates the negative lead of the capacitor. Note also that in an electrolytic capacitor, the negative lead is also shorter than the positive one.

Let’s now take a look at the ceramic capacitors. These capacitors are too small for full labels. Instead, they use a three digit code and their unit is always expressed in picofarads, or pF. The first two numbers are the value, and the third number indicates how many zeros you have to add to the previous two digits to provide their value in picofarad.

Additionally, when the number of picofarads is very small, in the order of only one or two digits, then the value can be directly expressed with those digits. In that case, we have only one or two digit numbers.

For example, on this one we read the digits 1-0-4. That means we have a 10 followed by 4 zeros. That gives us the number 100,000, so the value is 100,000 pF, or 100nF, or 0.1uF. And yes, we need a little math to interpret the values of these capacitors.

Here is another ceramic capacitor. This one has only two digits printed on it: 3-3. This means that the number 33 is the nominal value of the capacitor in pF.

Lastly, let’s take a look at a film capacitor.

These capacitors often use a mix. You might see a 3-digit code, like the ceramics, but you will also see a letter at the end. That letter represents the tolerance, or how accurate the nominal value actually is.

But wait, there is more: the rated voltage. This one can be expressed in three different ways. It can be written explicitly, or it could be missing, of there could be a code which is prefixed to the capacitor value.

If it is expressed in clear, then that is the actual rating.

If the voltage rating is not present at all, then it is 50V by default.

If it is encoded along with the capacitance value, then it can be one of those listed in the EIA standard. Here is the corresponding table for the most common.

As an example, the film capacitor above reads: 2A393J.

2A translates into a voltage rating of 100V; 393 translates into a value of 39,000pF, or 39nF, and the letter J at the end translates into a tolerance of 5%.

Here is the hole list of tolerances.


A pro tip for you now, valid for any kind of capacitor. If the text is rubbed off, or too small to read, or has any other problem that prevents you from reading it, don’t guess. Use a multimeter capable of reading capacitance. It will give you the live reading of exactly what that component is holding, and it’s the only way to be 100% sure before you solder the component in a circuit.

Pitfalls


Okay, now that we have covered some theory and some practical aspects, it’s time to take a look at what I call the ‘Wall of Shame’. If you stay in this hobby long enough, you will eventually blow up a capacitor. It’s almost a rite of passage! But to save you the jump-scare and the smell of burnt electrolyte, I want to show you the most common ways people accidentally kill or misuse their capacitors—and how you can avoid doing the same.
Here is my list #1 mistakes every beginner makes and how to fix or prevent them.

  • The polarity POP or: connecting an electrolytic capacitor backward. The consequence is that the internal dielectric breaks down, the electrolyte boils into gas, and pressure builds up until the safety vent bursts, or the whole capacitor pops. To prevent that, always look for the stripe on the side of the capacitor, which marks the negative lead, or look for the longer leg, which marks the positive lead.
  • Ignoring the voltage rating, or using a capacitor that is rated exactly for the voltage of the circuit or. worst, a capacitor with a smaller rating. In such a case, an excessive voltage can push the capacitor over its limits, causing it to leak or fail prematurely. Avoid that by always leave a safety margin. Use a capacitor rater 20 to 50% higher than the circuit voltage. If the circuit works at 12V, use a 16V or even a 25V capacitor.
  • The ghost charge. This has more to do with safety. Don’t assume a capacitor is off just because the device is unplugged. Capacitors, especially if large, can hold a dangerous charge for days or even weeks. Touching the leads can give you a nasty shock, or damage the multimeter if connecting the charged capacitor to it. Before handling the capacitor, discharge it. This can be safely done using a high value resistor ,like 1k, to bleed the energy off slowly.
  • Wrong type for the job, for example when using an electrolytic capacitor when a ceramic one should have been used instead. The result is usually an erratic behavior of the circuit. For example, using a large electrolytic capacitor near a micro-controller can cause the random reset of the micro-controller itself, because of the random electrical noise on the power line that the capacitor cannot get rid of. In such a case a small ceramic capacitor should be used for decoupling. Remember: electrolytic capacitors are good for bulk energy storage, ceramic capacitors are good for high speed noise filtering.
  • Soldering stress, or thermal shock. Holding the soldering iron on the capacitor leads for too long causes excessive heat that can dry out the electrolyte inside an electrolytic capacitor, of crack the ceramic layer of a ceramic capacitor, or melt the dielectric of a film capacitor. Always use a clean and tinned iron tip to be able to do make good soldered joints is a short time. You may want to see my video on soldering techniques for further information.

The Essential Capacitor Starter Kit

Before closing, here are some suggestions to create your own capacitors starter kit, an assortment of capacitors that covers 95% of the necessities for beginners projects, like Arduino, LED circuits, simple audio circuits, and so on. Start with a mix of ceramic and electrolytic capacitors. You can add more later.


Ceramic capacitors will be useful as non polarized noise killers. They are used for decoupling and filtering high frequency noise.
Useful values are:

  • 22pF, essential if you are building your own micro controllers, ad they are used in crystal oscillators.
  • 0.1 uF, the most common capacitor in existence. Every integrated circuit usually needs one of these right next to its power pin.
  • 1uF, good for general purpose filtering


Electrolytic capacitors will be useful as polarized power smoothers. These are bulk energy storage for power supplies. The most common values for beginner projects are:

  • 10uF, 25V or 50V. used for small scale power smoothing.
  • 100 uF, 25V. Great for stabilizing power rails in breadboard projects.
  • 1000uF, 25V. The big tanks. Used when dealing with motors or long LED strips of LEDs that pull a lot of current.

As an alternative, rather than buying individual values, search for capacitor assortment kits, on sites like Amazon, Adafruit, or Ali Express. They usually come in a plastic organizer box and are very cheap.

When buying a kit, look for capacitors rated at 25V or 50V. While 16V capacitors are smaller, a 50V capacitor can do everything a 16V one can, making it much more versatile for a beginner who might accidentally plug it into a 24V source.

Conclusion


So, there you have it: the humble capacitor. It is not just a tiny battery; it is the heartbeat and the filter of almost every circuit you’ll ever build.

I’ll see you in the next episode, and in the mean time…

Happy experiments!!!

Back To Basics Episode 5: Kirchhoff’s Laws – The Rules Of Circuits

Welcome back to Back To Basics, our journey to master electronics one little bit at a time.

So far, we have covered the essentials: safety, basic tools of the trade, and the important Ohm’s law, the foundational relationship between voltage, current, and resistance.


But what happens when circuits get more complex than a single resistor? What about parallel branches, multiple power sources, or a complex resistive network? We need a bigger, better set of rules. Today, we’re introducing the two most powerful, indispensable rules in circuit analysis: Kirchhoff’s Laws.

Named after physicist Gustav Kirchhoff, these laws are the foundation for everything we do next. By the end of this video, you’ll be able to analyze any basic series or parallel circuit and understand how energy and charge are conserved inside the wires.

KCL

Let’s start with the simplest concept, the one you can’t argue with: Kirchhoff’s Current Law, or KCL. KCL is all about the conservation of electric charge. It states that: The algebraic sum of currents entering a node (or junction) must be equal to the algebraic sum of currents leaving that node.


Think of it as a plumbing pipe junction, or a traffic merge lane. If you have 5 Amperes of current flowing into the junction, you must have 5 Amperes flowing out across all the outgoing paths. Charge can’t just pile up or disappear in a wire—it must be conserved. Simply put: What comes in must come out!


We call the meeting point of three or more wires a node. Mathematically, we express this as: The sum of currents entering the node equals the sum of currents leaving the node.


Let’s look at this simple parallel circuit.


We have a total current It leaving the battery. When it hits the first parallel junction (the node), it splits into two branch currents, I1 and I2. KCL immediately tells us that the total current is the sum of the branch currents.


So, It = I1 + I2. And here is the clever part: at the next node, I1 and I2 meet up again to form the original total current It, as it returns to the battery. KCL is your sanity check for all parallel circuits.

KVL


Let’s now talk about the other law, which is about the principle of energy conservation in a circuit: Kirchhoff’s Voltage Law, or KVL.
KVL governs the voltages around a closed loop—any path that starts and ends at the same point.


KVL states that: The algebraic sum of all the voltages around any closed loop in a circuit is equal to zero.


To understand the meaning of this statement, let’s use another analogy. Imagine a roller coaster, which works based on the physics concept of potential energy. The battery (the voltage source) is the lift hill that gives the car potential energy—a voltage rise. The resistors are the dips, loops, and brakes that use up or drop that energy—the voltage drops. When the car returns to the loading platform, its net change in height—its net potential energy—is zero.


In a circuit loop, the energy supplied by the source must be completely dropped across the components. If we trace the entire loop, the sum of voltage rises and drops must be zero.


In this simple series circuit, we have a source voltage (VS) and three resistors with voltage drops V1, V2, and V3 across them. If we trace the loop, always in the same circular direction representing the flow of the current, going from the negative to positive terminal of the battery is a rise, and going across each resistor in the direction of current flow is a drop.


KVL says:
Vs -V1 – V2 – V3 = 0


Rearranging this equation shows us that the source voltage is exactly equal to the sum of the voltage drops:
Vs = V1 + V2 + V3


KVL is the reason why the voltage splits up in a series circuit. The total energy has to be accounted for, and it must balance out to zero when you return to the start. If your KVL equation doesn’t equal zero, you’ve made a mistake!

Circuit Analysis Application


Now for the fun part: let’s put KVL, KCL, and our trusty Ohm’s Law together. This is where you unlock your circuit analysis superpower.


Here is a classic intermediate circuit: a series resistor, followed by two parallel resistors, all connected to a battery. We cannot simplify this down to a single equivalent resistance as easily. So… what do we do?

First, we look at the main node where the total current (IT) splits. KCL immediately gives us our first equation:

It = I2 + I3


Next, we apply KVL to the main loop. We have one voltage rise (Vs) and three drops: across R1, R2, and R3. Wait, we only need to account for the components in the loop.

Let’s apply KVL to the outer path: The source voltage minus the drop across R1 minus the drop across R2 must equal zero.

Vs – VR1 – VR2 = 0


And here’s the trick. We use Ohm’s law, V = IR, to replace the voltage drops with their corresponding currents and resistances.

Since It flows through R1 and I2 flows though R2, our final KVL equation becomes:

Vs – (It * R1) – (I2 * R2) = 0

Now we have two equations,

It = I2 + I3 and

Vs – (It * R1) – (I2 * R2) = 0


and we can create a third for the second inner loop:


Vs – (It * R1) – (I3 * R3) = 0


By substituting and solving this system of linear equations, we can find any unknown current or voltage in the circuit! This is the power of Kirchhoff’s Laws.

Conclusion


Today, we have learned that all complex circuits follow two simple, unbreakable rules: Charge is conserved (KCL), and energy is conserved (KVL). These are the cornerstone principles that every electrical engineer and technician uses daily.


In the next episode of Back To Back, we are going to examine a new component that can be used in electronic circuits: the capacitor. From there, a whole new world will open to us, filled with voltages and currents that change over time and can be used for many, many applications.


Happy experiments!!!

Companion Video: