Tag: Electronics

Deep Dive into the Theremin v.2 Audio Amplifier

See YouTube video https://www.youtube.com/watch?v=90T0ZkN-oos&t=3s for further details.

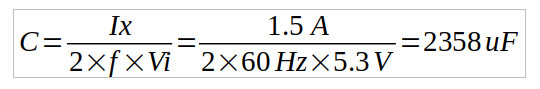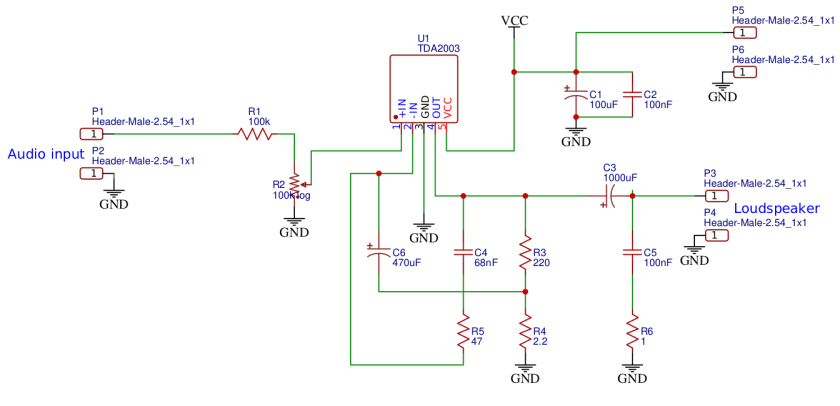
audio_amp_schematic

The Theremin v2 audio amplifier and preview audio amplifier share the same schematic.

The input of the amplifier is on pins P1 and P2, where P2 is the ground connection. The input is supposed to be DC decoupled with a small electrolytic capacitor, as suggested by the data sheet of the integrated circuit TDA2003, which is the main component of this amplifier. However, the capacitor was not put in this schematic because it will find its place directly on the output of the audio generator stage. No reason to have two capacitors in series: one at the output of the audio generator and one at the input of the audio amplifier.

The signal coming from P1 goes to a voltage divider consisting of the resistor R1 and the potentiometer R2. When the potentiometer cursor is all the way toward ground, there will be no signal going to pin 1 of the IC and, therefore, the amplifier will be silent. When the potentiometer cursor is all the way toward resistor R1, the signal coming from P1 is divided exactly in half, since the value of the potentiometer R2 and of resistor R1 are exactly the same. This is the position where the volume will be the maximum possible.

I chose the value of 100K for both R1 and R2 so to have a relatively high impedance toward the audio generator, so its output won’t be affected by the movement of the potentiometer. At the same time, I wanted a value of R2 low enough to keep the input of the amplifier solidly on the ground when there is no input signal.

R2 is a logarithmic potentiometer, which means that its value changes according to a logarithmic scale. This is done to compensate for how we perceive the sound volume: the potentiometer increases the power of the sound wave in the opposite way as our ear perceives it. This way, we feel that the volume increases and decreases linearly when we turn the potentiometer.

The output from pin 4 of the IC goes to the loudspeaker through capacitor C3, which is used to prevent that a DC current goes all the way through. In addition, capacitor C5 and R6 provide a high pass filter that shorts to ground all the high frequencies that are not supposed to go to the loudspeaker. Values of capacitors C3 and C5 and the resistor R6 reflect the suggestion on the data sheet.

data_sheet_schematic

The power supply comes in through pins P5 and P6 and is filtered by capacitors C1 and C2.

C2 takes care of shunting toward ground any unwanted high frequency signal coming from/to the power supply. Capacitor C1, which is a high value electrolytic capacitor, is mostly used to boost the input current when the amplifier requires sudden increases due to peaks of the volume. These capacitors have also the values suggested by the data sheet.

The last part of the amplifier is the negative feedback loop, connected between pins 4 and 2 of the TDA2003. The loop is composed of capacitors C4 and C6, and the resistors R3, R4, and R5.

The negative feedback is used to limit the output power of the amplifier outside the region of frequencies where it is requested, thus preventing auto oscillations of the amplifier, which would otherwise behave like an oscillator.

The values of these components are again those suggested by the data sheet. However, C4 and R5, which correspond to Cx and Rx in the data sheet, are calculated based on the data sheet formulas visible in the above picture, where B is the maximum frequency of the signal that we want to amplify, which I set to 10kHz. I don’t believe we want to hear from the Theremin sounds that are above that frequency.

For further information on this amplifier and for a demonstration on how it works, please refer to my corresponding YouTube video.

A Tester For Zener Diodes

Zener diodes are used for several purposes, from providing a reference voltage, to protecting sensitive circuits from being destroyed by the wrong input.

Today, I will show you how these diodes work and how to build a simple circuit to measure their most important characteristic, the reverse breakdown voltage. To know more on this topic, please watch the companion video posted on YouTube.

A zener diode looks like a regular diode and actually behaves as such when directly biased (positive voltage on the anode).

However, when inversely biased (negative voltage on the anode), a zener diode behaves in a completely different way.

Let’s take a look at its characteristic I-V diagram:

zener_characteristic

You can see that in the region of direct (or forward) bias, the zener behaves just like any diode. It also seems like in the inverse bias it behaves like a regular diode.  However, there is a big difference between the two.

For a regular diode, the reverse breakdown voltage is very high, in the order of 100V or more, sometimes much more. Such high that you never think at it when you use regular diodes, and you assume that with inverse bias the diode just does not conduct electric current.

For a zener diode, instead, the reverse breakdown voltage is low, in the order of one or two digit volts. Therefore, it is very easy in an electronic circuit to bring this kind of diode to reach the condition when it will start conducing electric current even if inversely polarized.

We actually exploit this behaviour to create reference voltages, or to provide a protection against unwanted voltages at the input of certain circuits, or a ton of other things.

The behaviour of a diode depends in fact upon the way it was fabricated, and in particular upon how it was doped. Regular diodes are lightly doped, while zener diodes are heavily doped. Depending on the amount of doping on both the P and the N side of the junction, the reverse breakdown voltage changes. That way, manufacturers can create zener diodes within a large range of breakdown voltages.

Problem is, manufacturers often don’t put the value of the breakdown voltage on the body of the components. Instead, they put some internal code or, sometimes, nothing at all.

So, if you had a number of such diodes on your workbench, how to distinguish them from one another?

Meet the zener tester.

It is a device that allows you to measure the reverse breakdown voltage, so you know if the diode works and what that voltage is.

How such a tester works? From the I-V diagram above, you can see that the characteristic of the zener diode is an almost vertical line when polarized in the reverse bias region. For any current value in that vertical line, the voltage is always the same and corresponds to the breakdown voltage. So, if we circulate a current at any point of that vertical line, we can measure at the terminals of that diode its breakdown voltage.

The zener tester I’m showing you today does just that: forces a current into the zener diode so we can measure the value of the breakdown voltage. We choose this current in such a way that it is high enough to stay away from the point where the characteristic is not linear, but low enough to avoid dissipating inside the diode a power that the diode itself cannot handle.

The following link allows you to download an archive containing the schematic of such device, along with the OpenSCAD code to 3D print the box for the device.

zener_diodes_tester_files

In the schematic you’ll see that I used a ready-made boost converter and a digital voltmeter. Here are the links to the store where I bought them. Of course you are free to use any other equivalent component. It will work as well.

BOOST CONVERTER

DIGITAL VOLTMETER

Please make sure to watch the YouTube video that completes the information I provided in this post. Between the two, you should have a complete view of the design of the device and should be able to build it.

Happy experiments!

 

Theremin v.2 Power Supply Design

theremin-v2-power-supply

For the new version of the Theremin, I have chosen to use a dual 12V power supply. This will have more flexibility because it will allow me to use more sophisticated units, possibly using op-amps.

The circuit is very basic: it uses a dual 14V transformer (not shown in the schematic) capable of providing 1.5A at its output.

A dual transformer is made up as in the following picture.

center-tapped-transformer

Is has a primary winding that is connected to the AC power supply outlet, and a secondary winding with a center tapped wire that is usually put to ground on the low voltage circuit side.

Voltage between either end wire of the secondary and the center tapped wire is usually the same (with the exception of specifically made transformers), which we call V.

The voltage measured between the two end wires of the winding is instead two times V or 2V.

Sometimes, instead of having a single secondary winding, we have two, carrying the exact same voltage. In this case, we can connect together the two closest wires and consider that as the center tapped wire. Then everything works as the first kind of transformer.

transformer-trans64

The AC current of the transformer is converted in to a DC current through the usage of a bridge rectifier and the capacitors C1 and C2.

The bridge rectifier converts the sine wave coming from the transformer into a fully rectified wave.

Full-wave_rectified_sine

Then, the capacitor that follows (in this case C1 and C2) starts charging over the ascending sides of the wave and discharging, partially, over the descending sides of the wave, basically filling the wave in between crests and making it look like more a straight horizontal line with some disturbance in it that we call ripple (the red line in the following picture).

ripple

In general, depending on the use of the power supply, we define a maximum value of the ripple that the circuit can handle.

In our case, we need to make sure that the voltage at the input of the regulators never goes below 14.5V, according to the data sheet, otherwise the regulator will not function properly.

The peak voltage provided by the transformer is its RMS value multiplied by the square root of 2, or:

peak_voltage

The minimum voltage we can have at the input of the regulator is:

regfulator_input_voltage

This is the max value of ripple that we can sustain.

To calculate the capacitor necessary to obtain this ripple, we use the following formula:

capacitance calculation

where f is the frequency of the alternate current which, in the USA, is 60Hz, and Ix is the maximum current that the power supply needs to provide.

So, we would need a capacitance value, for C1 and C2, of 2358uF.

However, the Theremin circuit will really not draw 1.5A from the power supply, so we can stay a little conservative, and use the closest value below the calculated one, which is 2200uF.

At this point we can safely say that the voltage on the output of the regulators will be exactly 12V (positive or negative, depending on the output side).

To further help the regulator, and preventing the current through it to go too close to the 1.5A threshold, where the regulator would not work anymore because the ripple becomes too high, we add to the output of each regulator another electrolytic capacitor, this one with a value at least equal to the capacitance value that we did not put at the input side. Since at the input side we put a capacitance of 2200uF instead of 2358uF, we will need a capacitor of at least 158uF.

However, to stay totally safe, I decided to use a capacitor at least 5 times higher, so I used the value of 1000uF for C3 and C4.

And finally, I added an extra capacitor (C5 and C6) to shunt toward ground any RF frequency that would travel back from the Theremin oscillators toward the power supply. A 0.1uF value is what is suggested by the data sheet of the regulator, so I used just that.

Why did I use this capacitor if there was already a 1000uF in there?

The reason hides in the way the electrolytic capacitors behave. In short, the electrolytic capacitors do not work well at high frequencies, so we need to add the extra 0.1uF capacitor, which is not an electrolytic one, to work in that range of frequencies. And since the range of frequencies is much higher than the one of the 110Vac outlet, a very small capacitance is enough to do the job.